Abstract
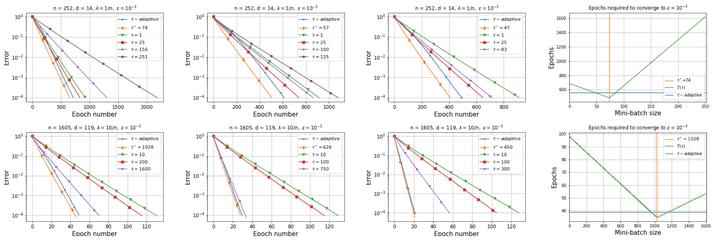
Recent advances in the theoretical understanding of SGD led to a formula for the optimal batch size minimizing the number of effective data passes, i.e., the number of iterations times the batch size. However, this formula is of no practical value as it depends on the knowledge of the variance of the stochastic gradients evaluated at the optimum. In this paper we design a practical SGD method capable of learning the optimal batch size adaptively throughout its iterations for strongly convex and smooth functions. Our method does this provably, and in our experiments with synthetic and real data robustly exhibits nearly optimal behaviour; that is, it works as if the optimal batch size was known a-priori. Further, we generalize our method to several new batch strategies not considered in the literature before, including a sampling suitable for distributed implementations.
Motasem Alfarra
PhD Candidate - Electrical and Computer Engineering
I am a Ph.D. candidate at KAUST in Saudi Arabia. I am part of the Image and Video Understanding Lab (IVUL) advised by Prof. Bernard Ghanem. I obtained my M.Sc degree in Electrical Engineering from KAUST, and my undergraduate degree in Electrical Engineering from Kuwait University. I am interested in test-time adaptation and continual learning. Previously, I worked on assessing and enhancing network robustness and leveraging robust models for different applications.