Abstract
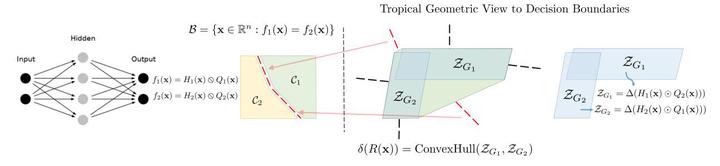
This work tackles the problem of characterizing and understanding the decision boundaries of neural networks with piecewise linear non-linearity activations. We use tropical geometry, a new development in the area of algebraic geometry, to characterize the decision boundaries of a simple network of the form (Affine, ReLU, Affine). Our main finding is that the decis on boundaries are a subset of a tropical hypersurface, which is intimately related to a polytope formed by the convex hull of two zonotopes. The generators of these zonotopes are functions of the network parameters. This geometric characterization provides new perspectives to three tasks. (i) We propose a new tropical perspective to the lottery ticket hypothesis, where we view the effect of different initializations on the tropical geometric representation of a network’s decision boundaries. (ii) Moreover, we propose new tropical based optimization reformulations that directly influence the decision boundaries of the network for the task of network pruning. (iii) At last, we discuss the reformulation of the generation of adversarial attacks in a tropical sense. We demonstrate that one can construct adversaries in a new tropical setting by perturbing a specific set of decision boundaries by perturbing a set of parameters in the network.
Motasem Alfarra
PhD Candidate - Electrical and Computer Engineering
I am a Ph.D. candidate at KAUST in Saudi Arabia. I am part of the Image and Video Understanding Lab (IVUL) advised by Prof. Bernard Ghanem. I obtained my M.Sc degree in Electrical Engineering from KAUST, and my undergraduate degree in Electrical Engineering from Kuwait University. I am interested in test-time adaptation and continual learning. Previously, I worked on assessing and enhancing network robustness and leveraging robust models for different applications.